yismxplusc: Geometric proof of DIFFERENCE OF TWO SQUARES

Friday 8 June 2018

Geometric proof of DIFFERENCE OF TWO SQUARES

GEOMETRIC PROOF OF THE DIFFERENCE OF TWO SQUARES

The difference of two squares states that for all numbers $a$ and $b$ , $a^2 - b^2 = (a + b)(a-b)$ .
The visual representation below, however, only covers the condition that $a^2 - b^2 \geq 0$

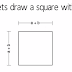
To proceed with the visual proof, we create a square with side length $a$ as shown in (1). Then, we cut a square with side length $b$ from its corner as shown in (2). Since the area of the larger square is $a^2$ and the area of the smaller square is $b^2$ , the area of the remaining figure is $a^2 - b^2$ .
Next, we draw a horizontal line segment cutting the remaining figure into two rectangles as shown in (3). We change the color of the smaller rectangle for clearer representation, and move it to the right hand side as shown in (4).